Hallo "Ph0b0ss",
es gibt "massenhaft" Programme, mit denen man alle möglichen Konfigurationen unterschiedlichster Filter ausrechnen kann.
Aber eigentlich nützen sie nicht so viel, wenn man nicht ständig damit zu tun hat....
Ich halte es für viel wichtiger, die grundsätzlichen "Eckdaten" im Auge zu behalten:
- * Üblicherweise haben Filter um so höhere Gruppenlaufzeiten, je steiler sie sind und je tiefer die Übergangsfrequenzen liegen.
* Filter mit "einem sanften Übergang" zwischen dem "linearen Bereich" und der "vollen Steilheit" haben entweder keinen oder nur einen kleinen Anstieg der Gruppenlaufzeit in der Nähe der Eckfrequenz (zum Beispiel "Bessel"-Tiefpass-Filter).
* Je schärfer ausgeprägt der "Knick" im Frequenzgang ist, desto größer wird der Anstieg der Gruppenlaufzeit im Bereich der Eckfrequenz.
Ein Tschebyscheff-Tiefpassfilter 8. Ordnung (also 48 dB/oct), bei dem 0.1 dB "Frequenzgang-Welligkeit" im Durchlass-Bereich erlaubt ist, hat theoretisch knapp 41 ms delay bei knapp 83 Hz. Wenn 1 dB Welligkeit erlaubt ist, hat der Frequenzgang einen
noch schärferen Knick zwischen dem Durchlass- und Sperrbereich - dafür steigt aber die Gruppenlaufzeit aber schon auf über 60 ms bei 80 Hz.
In der Praxis können die theoretischen Werte bei Tschebyscheff-Filtern (in der Serie) kaum exakt erreicht werden, weil man dazu extrem enge Bauteile-Toleranzen benötigen würde.
Hier Messdiagramme mit Frequenzgang und delay unterschiedlicher Tiefpass-Filtertypen:
(Wenn die Darstellung zu klein erscheinen sollte, mit der Maus in's Bild gehen und den Button "auf reguläre Größe erweitern" anklicken.)
http://www.nubert.net/g-nubert/Frq_80Hz ... scheby.png
http://www.nubert.net/g-nubert/delay_80 ... scheby.png
Pro Filter-Ordnung dreht sowohl ein Hochpass als auch ein Tiefpass (an der Eckfrequenz) die Phase um je 45°.
Bei einem Filter 4. Ordnung dreht also der Tiefton-Kanal die Phase um 4x45=180°. Das gleiche macht der Hochton-Kanal.
180+180° ergeben dann also (zumindest im "eingeschwungenen Zustand") mit 360° wieder Gleichphasigkeit.
(Mit DSP-FIR-Filtern kann man die Gruppenlaufzeiten und Phasenlage unabhängig von Frequenz und Steilheit einstellen. - Dabei handelt man sich allerdings eine (lineare) "Grundverzögerung" ein, die etwas über dem delay analoger Filter liegt.)
Ohne ein tieferes Verständnis der Filtertheorie sind die hochkomplexen Rechenprogramme nicht sehr geeignet, um damit "Alltagsprobleme" zu lösen - und sie sind schon gar nicht anwendungsfreundlich. (Für Matlab braucht man m.E. enorme Einarbeitungszeiten...)
Recht leicht zu handhaben ist ohnehin fast nur die "-6 dB-Sonderversion" des Butterworth-Filters, die man als "Linkwitz-Riley-Filter" bezeichnet. Sie hat im Tiefton- Hochton- und Summensignal die selbe Phasenlage und das Summensignal hat einen perfekt linearen Frequenzgang. Die Tiefpass- und Hochpass-Frequenzgänge "überkreuzen" sich dabei im "-6 dB-Punkt". (Bei den "normalen" Butterworth-Filtern überkreuzen sie sich im -3 dB-Punkt.)
Bei Filtern 2. Ordnung (also 12 dB / Oktave) muss man (von der Theorie her) Hoch- oder Tiefton-Kanal invertieren, um einen Frequenzgang ohne "Phasen-Auslöschungen" zu erzielen. Bei Filtern 4. Ordnung (oder einem Vielfachen davon) erfolgt die Summierung ohne Verpolung.
Die Grundlagen zur Filter-Theorie sind z. B. auch sehr schön in meinem Lieblingsbuch "Tietze Schenk - Halbleiter-Schaltungstechnik" erklärt, das wohl in jeder besseren Stadtbibliothek vorhanden ist.
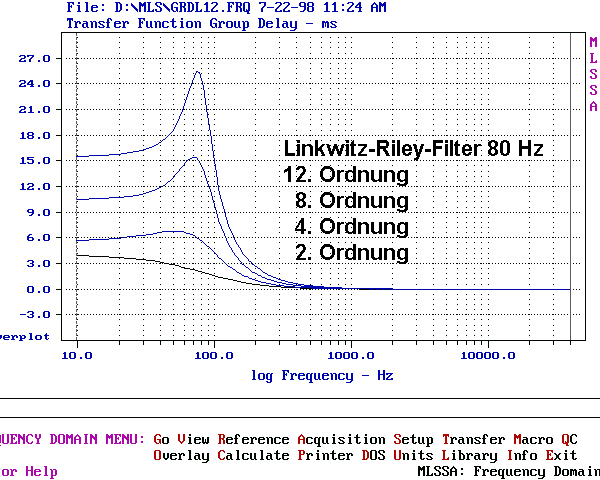
Zum Schluss noch zwei MLSSA-Messungen mit den group delay-Unterschieden zwischen Linkwitz-Filtern und Bessel-Tiefpass-Filtern unterschiedlicher Steilheit.
Die Gruppenlaufzeiten von Bessel-Tiefpass-Filtern sind "schön linear". Allerdings unterscheiden sie sich von den Werten der Hochpass-Filter und des Summensignals. Außerdem bringen Bessel-Filter (in der Grundform) oberhalb etwa 4. Ordnung keine ordentliche "Frequenzgang-lineare Summierung" des Hoch- und Tiefton-Kanals.
Die Dimensionierung eines Hochpass-Filters, das
so mit einem Bessel-Tiefpass höherer Ordnung "harmoniert", dass sich ein guter Summen-Frequenzgang ergibt, ist allerdings
tatsächlich eine Aufgabe für ein leistungsfähiges Computerprogramm!
Gruß, G. Nubert